Question :

Create a 100-bit binary ripple-carry adder by instantiating 100 full adders. The adder adds two 100-bit numbers and a carry-in to produce a 100-bit sum and carry out. To encourage you to actually instantiate full adders, also output the carry-out from each full adder in the ripple-carry adder. cout[99] is the final carry-out from the last full adder, and is the carry-out you usually see.

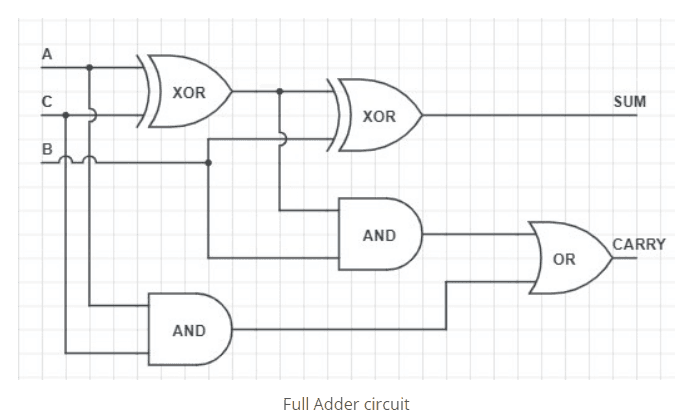
Step 1: Designing a 1-bit Full Adder

Before implementing a 100-bit Ripple Carry Adder, we need to build its fundamental building block: the 1-bit Full Adder. A Full Adder is a combinational circuit that performs binary addition on three inputs:

• A → First operand bit

• B → Second operand bit

• Cin → Carry-in from the previous bit

It produces two outputs:

• Sum → Result of bitwise addition

• Cout → Carry-out to the next stage

• Sum = A⊕B⊕Cin

• Cout = (A⋅B)+(B⋅Cin)+(Cin⋅A)

Verilog Code for a 1-bit Full Adder:

module one_bit_FA (
    input a, b, cin,   // Inputs: Two operand bits and carry-in
    output cout, sum    // Outputs: Sum and carry-out
);
    assign sum  = a ^ b ^ cin;  // XOR operation for sum
    assign cout = (a & b) | (b & cin) | (cin & a);  // Carry-out logic
endmodule

Step 2: Using the GENERATE Block to Create a 100-bit Ripple Carry Adder

Now that we have designed a 1-bit Full Adder, the next step is to chain 100 full adders together to create a 100-bit Ripple Carry Adder.

Since manually instantiating 100 full adders would be inefficient, we use a generate-for loop block in Verilog. This allows us to create multiple instances of a module dynamically.

Understanding the generate Block in Verilog

The generate block in Verilog is a powerful construct that allows you to replicate hardware structures based on a loop index.

• It is executed at compile time, meaning it generates hardware descriptions before synthesis.

• It is useful when multiple instances of a module are required, such as in adders, multipliers, and memory structures.

• It works with a special type of variable called genvar, which is used only inside generate blocks.

Step 3 : Verilog Code for 100-bit Ripple Carry Adder Using generate Block

module top_module( 
    input [99:0] a, b,
    input cin,
    output [99:0] cout,
    output [99:0] sum
);

    genvar i; // Declaring genvar variable

    // Instantiating the first full adder separately
    one_bit_FA FA1(a[0], b[0], cin, cout[0], sum[0]);

    // Generate 99 more full adders dynamically
    generate
        for (i = 1; i < 100; i = i + 1) begin : Full_Adder_Block// Block label
            one_bit_FA FA(a[i], b[i], cout[i-1], cout[i], sum[i]);
        end
    endgenerate

endmodule

How Verilog Assigns Names to Instances in generate Block

Each module instance inside the generate block gets a unique name based on the block label (Full_Adder_Block) and the loop index (i).

💡 Generated Instance names:

• top_module.Full_Adder_Block[1].FA

• top_module.Full_Adder_Block[2].FA

• top_module.Full_Adder_Block[3].FA

• ...

• top_module.Full_Adder_Block[24].FA → (This is the 25th full adder, i = 24)

• ...

• top_module.Full_Adder_Block[99].FA

Final Takeaway

🚀 Always label your generate blocks using begin : label_name for better hierarchical organization.
🚀 This method ensures proper instance naming for debugging and simulation.
🚀 Helps in large-scale digital designs like adders, multipliers, and pipeline processors.

Practice Exercise:

1️⃣ Write a Testbench:

• Instantiate the top_module.

• Declare reg and wire variables for inputs and outputs.

• Initialize test cases inside an initial block.